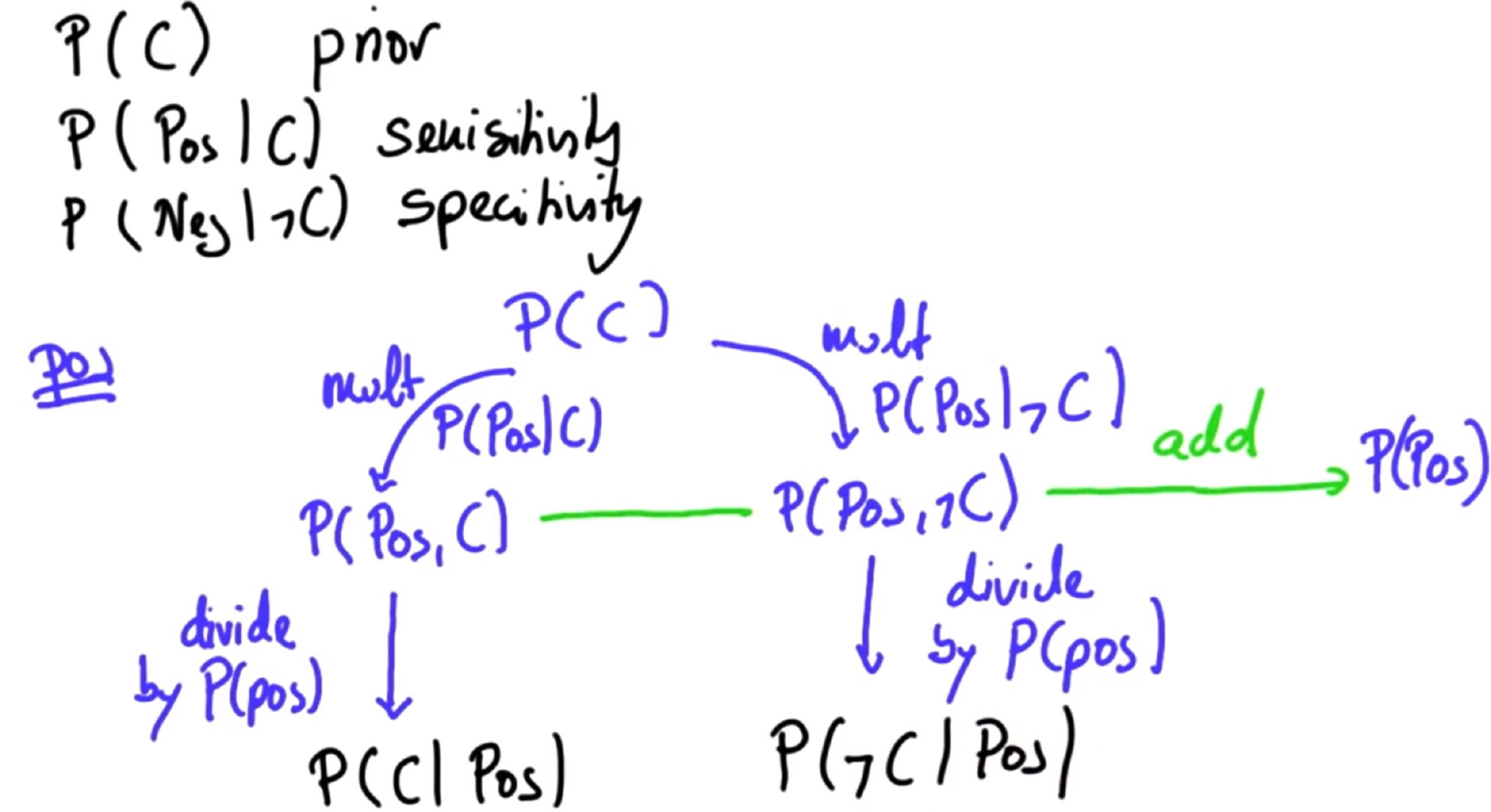
贝叶斯定理允许我们通过合并新的证据 （来自观察的数据或测试）并形成新的 后验 概率，从而提高 先验 概率。这一点可通过一系列的数学步骤来实现。
为了描述这些步骤，我会使用符号H进行假设（例如，汽车处于特定位置的可能性，或者人患有癌症的可能性等），并使用T表示测试观察结果/传感器数据（例如，汽车看到绿色或医疗检测结果为阳性）。例如， P(T|H)P(T|¬H) 是假设情形 没有 发生时产生传感器读数的概率。

关于符号

在解决这些问题时，您可能会看到其他符号，例如 P(H|T)P(H|T)、或P(X|U)P(X|U)、或
P(A|B)P(A|B) 等等，其中一个字母代表假设，另一个代表观察结果。符号不同，但概念相同。只要你对概念熟悉，你就能从容应对不同的符号！

1.先验概率

贝叶斯定理的第一步是确定任何先验概率。根据以前的数据，问一下自己，某个假设或特定事件 H发生的可能性有多大？

• 确定P(H)
• 得到P(H)后，即可推导出P(¬H)

2.条件/测试概率

通过收集的传感器或测试数据，你还应该知道，倘若假设H已经发生或没有发生，某个测试或传感器读数发生的可能性有多大。

• 确定P(T|H)和P(T|¬H)
• 得到P(T|H)后，即可推导出P(¬T|H)

步骤 1 和步骤 2 为你提供了执行贝叶斯规则所需的所有信息，并可以根据某些观察到的相关数据形成对假设可能性的预测。

3.联合概率

下一步是计算先验概率和测试概率的四个联合概率。下面给出了两个例子。

• P(H,T)=P(T|H)⋅P(H)
• 类似地,P(¬H,T)=P(T|¬H)⋅P(¬H)

4.总概率

然后，你需要确定测试结果或传感器读数的总概率，这样你就可以使用该值对后验概率（这是贝叶斯法则的最后一步）进行归一化。测试结果的总概率是测试结果发生的联合概率之和。下面是一个例子:

• P(T)=P(H,T)+P(¬H,T)

4.后验概率（最后一步）

然后，你需要确定测试结果或传感器读数的总概率，这样你就可以使用该值对后验概率（这是贝叶斯法则的最后一步）进行归一化。测试结果的总概率是测试结果发生的联合概率之和。下面是一个例子:

• P(H|T)= P(T|H)⋅P(H)/P(T)

​

问题：

贝叶斯法则不仅用于将传感器数据纳入估计过程，它也经常用于将测试数据纳入到医疗诊断中

• 在所有人口中，有1%得了癌症——P(C)=0.1
• 90%的癌症患者在接受癌症检测的血液检测结果为阳性，这意味着90%的可能性检测出癌症——P(Pos|C)=0.9
• 5%的人会有误报，也就是说有5%的可能性，会出现该检测在人们没有癌症的时候呈现阳性结果的情况——P(Pos|¬C)=0.05

鉴于上述数据，如果一个人的癌症检测结果为阳性，他患癌症的概率=P(C|Pos)=P(C)p(Pos|C)/[P(C)p(Pos|C)+P(Pos|¬C)[1-P(C)]]=0.6667